Coin change - solving dynamic programming in Elixir

Dynamic programming is a tough technique to master. You start with the obvious, like Fibonacci's sequence, but suddenly become overwhelmed when trying to sense the pattern and approach in other problems. In its sense it is quite simple, when you know what steps to follow.

In this article we'll tackle coin change, step by step, while leveraging awesome features of Elixir language.

Problem

Let's discuss the problem we're solving first.

Change in Elixir on Exercism

Can you solve Change in Elixir? Improve your Elixir skills with support from our world-class team of mentors.

Exercism

Our solution must correctly determine the fewest number of coins to be equal to the given target change from a given set of coins.

For example:

• An input of 15 with [1, 5, 10, 25, 100] should return [5, 10]
• An input of 40 with [1, 5, 10, 25, 100] should return [5, 10, 25]
• An input of 13 with [5, 10] should determine that you can't make the target change with a given coin set.

Intuition

First, we must come up with a decent proof, that this indeed is a problem for dynamic programming. We should check if there isn't a greedy approach first.

For the examples stated before, you can figure them all out going greedy - picking largest coin possible until you either run out of target, or have an amount smaller than your smallest coin, let's see first example:

target = 15, result = [], largest available coin is 10
target = 5,  result = [10], largest available coin is 5
target = 0,  result = [5, 10], correct result found

Seems like our greedy approach works! That's quite easy. But not so fast! You can actually prove that there are instances where greedy doesn't work, let's see this:

coins = [7, 6]
target = 12, result = [], largest available coin is 7
target = 5, result = [7], further change can't be made!

Instead our algorithm should try out the largest coin at first, but backtrack and try the second largest, too to check if there is a working or more optimal result in there. This smells like a recursion, let's design it with a brute-force approach first.

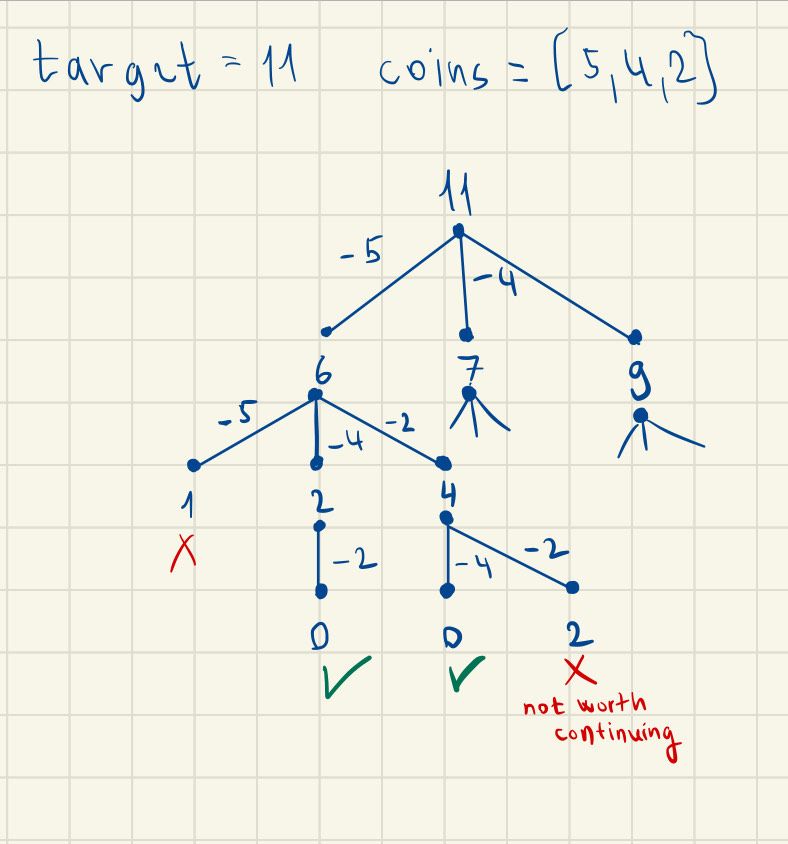
This is how our algorithm is supposed to look for optimal solution. It is of course not the whole tree, because the combinatoric explosion would be too messy to notice anything in.

We can notice one little flaw with this: we're getting to same results by multiple paths, like in the two that reached zero: [5, 4, 2] and [5, 2, 4]. What can we do about this?

We can actually keep coins sorted in a descending order, and once we "use" a certain coin in our solution path, we won't allow a larger coin to be used. This would mean, that with paths [5, 4, 2] , [5, 2, 4], [4, 5, 2], [4, 2, 5], [2, 4, 5], or [2, 5, 4] only the first one would be reached. That's a linear growth instead of a factorial growth, good for starters.

Let's write an example solution out of this!

defmodule Change do
  @spec generate(list, integer) :: {:ok, list} | {:error, String.t()}
  def generate(coins, target),
    do: {Enum.reverse(coins), Enum.max(coins)}
      |> then(fn {coins, max_coin} -> change(coins, target, max_coin) end)
      |> then(fn
        nil -> {:error, "cannot change"}
        change -> {:ok, change}
      end)

  defp change(_, 0, _), do: []
  defp change(coins, target, max_coin),
    do: (for coin <- coins, coin <= max_coin, coin <= target, reduce: nil do
            nil ->
              maybe_prepend(coin, change(coins, target - coin, coin))
            prev_change ->
              change = maybe_prepend(coin, change(coins, target - coin, coin))
              if change != nil and length(change) < length(prev_change), do: change, else: prev_change
        end)

  defp maybe_prepend(_, nil), do: nil
  defp maybe_prepend(item, list), do: [item | list]
end

There are numerous optimizations we can make to this algorithm:
- recursion is not tail call optimized, thus this does not scale very well, but only bottom-up recursion can work properly for our next enhancements
- we're still checking every possibility, the complexity, although drastically reduced still grows exponentially
- maybe_prepend helper is needed, but quite ugly

But we've done one thing greatly - at any given function call, the same parameters will return same values. That means that each time we try to find out what the optimal coin change for a target t is, we need the same value. This means we can cache the first computation and just return the cached value on repetitive calls.

This draws our complexity from exponential realm into quadratic one (approximately O(target*n)).

But how does one introduce this caching in a functional language such as Elixir without mutable state? Answer is surprisingly simple, just use the Process dictionary!

Now that we've got the right toolbox, let's modify the code:

defmodule Change do
  @spec generate(list, integer) :: {:ok, list} | {:error, String.t()}
  def generate(coins, target),
    do: {Enum.reverse(coins), Enum.max(coins)}
      |> tap(fn {coins, _} -> Enum.each(coins, &Process.put(&1, [&1]))  end)
      |> then(fn {coins, max_coin} -> change(coins, target, max_coin) end)
      |> then(fn
        nil -> {:error, "cannot change"}
        change -> {:ok, change}
      end)

  defp change(_, 0, _), do: []
  defp change(coins, target, max_coin),
    do: memoized(target, fn ->
      for coin <- coins, coin <= max_coin, coin <= target, reduce: nil do
          nil ->
            maybe_prepend(coin, change(coins, target - coin, coin))
          prev_change ->
            change = maybe_prepend(coin, change(coins, target - coin, coin))
            if change != nil and length(change) < length(prev_change), do: change, else: prev_change
        end
    end)

  defp memoized(target, fun),
    do: Process.get(target)
      |> then(fn
        nil -> fun.() |> tap(&Process.put(target, &1 || :none))
        :none -> nil
        memoized -> memoized
      end)

  defp maybe_prepend(_, nil), do: nil
  defp maybe_prepend(item, list), do: [item | list]
end

Now our algorithm works pretty well and is quite optimized for certain use-cases.

But generally, it's still pretty bloated, and we can surely do better. Namely, we need to convert our memoized recursion into a proper dynamic programming tabulation algorithm.

But how the hell does one do that? For me, after loads of dynamic programming problems it's still very hard when encountering new problem. You need to really visualize how the tabulation is done in the recursion, and do it iteratively.

So which values are filled-in first into the Process dictionary? Values of coins. So those are the first values we need to cache there. Then every target from 1 up to our target t either can be derived from some previous value, or is unreachable (change cannot be made from it with given coins).

So intuition is basically this: for any given target t, try every coin c in our coin set check for presence of target in memo[t-c] in our cache, and if it exists, add c to the value stored in memo[t-c], and memoize the result in memo[t]. If there is no cache for mentioned key, we simply ignore it, because change cannot be made.

After we do this for every target in range 1..t, our result will be cached in memo[t]. Quite unintuitive for an untrained eye, but, it is really that simple. Let's represent it in elixir!

defmodule Change do
  @spec generate(list, integer) :: {:ok, list} | {:error, String.t()}
  def generate(coins, target) do
    Process.put(0, [])
    Enum.each(coins, &Process.put(&1, [&1]))
    for t <- 1..target do
      for c <- coins do
        case {Process.get(t), Process.get(t-c)} do
          {nil, nil} -> nil
          {nil, val} -> Process.put(t, [c | val])
          {prev, curr} when length(prev) > length(curr) + 1 -> Process.put(t, [c | curr])
          {_, _} -> nil
        end
      end
    end

    case Process.get(target) do
      nil -> {:error, "cannot change"}
      val -> {:ok, val}
    end
  end
end

Looks neat, doesn't it? But there is a mistake that has been all along since we've introduced mutable state. Our Process dictionary won't tidy up after itself, and our result can possibly interfere with next calls of our generate.

This is our very own design issue from the BEAM point of view. Since one computation should be isolated from the caller process, we must spawn a Task specifically for it. For keeping the API stable, we'll make the generate a blocking call, but generally, it would be better for it to act as a Task, so we could make multiple generate calls in parallel more idiomatically.

defmodule Change do
  @spec generate(list, integer) :: {:ok, list} | {:error, String.t()}
  def generate(coins, target) do
    Task.async(fn -> change(coins, target) end)
    |> Task.await()
  end

  defp change(coins, target) do
    Process.put(0, [])
    Enum.each(coins, &Process.put(&1, [&1]))
    for t <- 1..target do
      for c <- coins do
        case {Process.get(t), Process.get(t-c)} do
          {nil, nil} -> nil
          {nil, val} -> Process.put(t, [c | val])
          {prev, curr} when length(prev) > length(curr) + 1 -> Process.put(t, [c | curr])
          {_, _} -> nil
        end
      end
    end

    case Process.get(target) do
      nil -> {:error, "cannot change"}
      val -> {:ok, val}
    end
  end
end

Perfection! Now the computation is isolated in its own BEAM process, just how god of Erlang has intended it!

Note that the memoized recursion could be optimized significantly - particularly in our image visualisation, there is a note that longer path then previously found optimum is not worth exploring, our algorithm explores it anyway. This could be done if we'd memoize how long is the "current" optimal change, but that's a very specific optimization and the memory footprint can be still huge in non-tail call optimized recursion.

Now interesting thing is that our dynamic programming algorithm resembles Dijkstra's algorithm - if we picture our coins as weighed edges in a graph, then we're trying to find the shortest possible path by rewriting the "current longest" one.