Sum of Subarray Minimums problem

I've tackled a problem which I found to be very problematic for me, so I've decided to make a detailed analysis of it here.

The problem can be found here: https://leetcode.com/problems/sum-of-subarray-minimums

Let's describe problem in more detail:

Given an array of integers arr, find the sum of min(b), where b ranges over every (contiguous) subarray of arr. Since the answer may be large, return the answer modulo109 + 7.

This means that for array [1,2,3] there are these contiguous subarrays:

[1,2,3]
[1,2]
  [2,3]
[1]
  [2]
    [3]

If we abstract it a bit we can simply make a proof that the number of contiguous subarrays grows quadratically in proportion to size of it.

This means that any algorithm which brute forces the solution will have O(n^2) time complexity.
As we can see the constraints, that will not be sufficient:
- 1 <= arr.length <= 3 * 104
- 1 <= arr[i] <= 3 * 104

But for the sake of completeness, we'll try to solve it this way.

The most intuitive way (at least for me) is to solve it by recursion, we can design a solution that divides this into subproblems, for example divide the array in two subarrays where we remove one item from start on first subarray and last item from end on second subarray.

Then we can determine the min up to trivial cases, like minimum of 1 element subarray, and then minimum of these two subarrays recursively. Here is the call stack of concrete example:

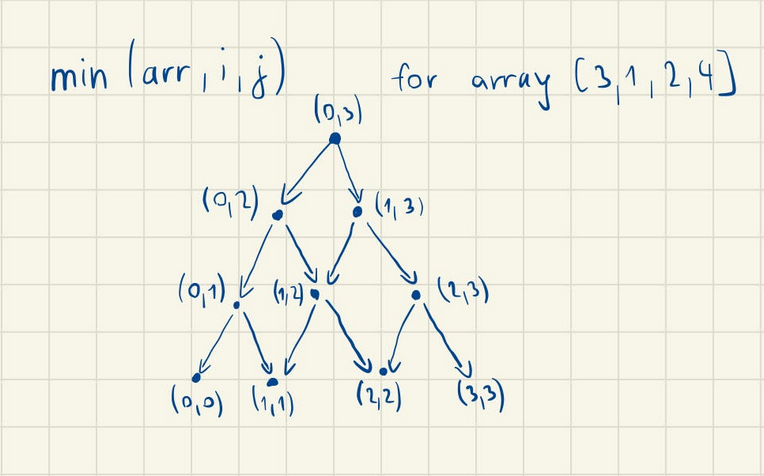
Code will look like this:

class Solution
{
    public function solve(array $arr): int
    {
        return $this->subarrayMin($arr, 0, count($arr) - 1);
    }

    private function subarrayMin(array $arr, int $i, int $j): int
    {
        if ($i === $j) {
            return $arr[$i];
        }

        return min(
            $this->subarrayMin($arr, $i, $j-1),
            $this->subarrayMin($arr, $i+1, $j),
        );
    }
}

This is a function that recursively finds minimum of a given subarray. We can work with this, but we need to prevent repetitive calls, because now its time complexity reaches O(2^n), which is a problem.

We also need to store the sum somewhere, but only on first computation, because we need to sum up only unique subarrays.

class Solution
{
    private const MOD = 1000000007;

    /** @var int[][] */
    private array $memo;
    private int $sum;

    /** @param int[] $arr */
    public function sumSubarrayMins(array $arr): int
    {
        $this->sum = 0;
        $this->memo = [];
        $this->subarrayMin($arr, 0, count($arr) - 1);
        return $this->sum;
    }

    /** @param int[] $arr */
    public function subarrayMin(array $arr, int $i, int $j): int
    {
        if (array_key_exists($i, $this->memo) && array_key_exists($j, $this->memo[$i])) {
            return $this->memo[$i][$j];
        }

        $this->memo[$i] ??= [];

        if ($i === $j) {
            $min = $arr[$i];
        } else {
            $min = min(
                $this->subarrayMin($arr, $i, $j-1),
                $this->subarrayMin($arr, $i+1, $j),
            );
        }

        $this->sum = ($this->sum + $min) % self::MOD;
        return $this->memo[$i][$j] = $min;
    }
}

This is a working solution, but as we stated earlier, too slow. We need to think about some math trick to do this smarter and faster. Remember the proof of array length. We can play around with that.

Let's see this array: [3,1,5,4]
What can we observe that could possibly help us?

• the minimum of item on index i is a minimum for all subarrays from the previous index p, where arr[p] < arr[i] up to next index n, there arr[n] < arr[i]
• if we knew this, we can compute the number of subarrays in which the given item is a minimum, and if we multiply it by the item value, we get it's contribution to the sum!

Let's test this hypothesis:

We can compute the range of this small array manually and it would ideally look like this:

arr   =  [3,1,5,4]
left  =  [0,0,2,2]
right =  [0,3,2,3]

With these values we compute result like this (pseudocode):

fn = x => (x * (x+1)) / 2
contrib[i] = fn(right[i]-left[i]+1) - fn(i-left[i]) - fn(right[i]-i)

But how the hell will we compute this left and right array in linear time ? Fortunately, there is a data structure to save us! It's monotonic stack.

It basically works like normal stack, but it keeps its values sorted. In our case we need the largest value on top. That means that if stack top is larger than our value, we need to pop it if we want to push our element. We'll explain it visually:

This is exactly how we compute the left array in O(n) time. And how do we compute the right array? The exact same way, but we'll iterate the array from end to start.

You may think that is all there is, but there is one other problem. What if our array would contain duplicate?

The solution was fortunately pretty easy, now there is the working result in PHP:

class Solution {
    private const MOD = 1000000007;

    /**
     * @param int[] $arr
     * @return int
     */
    function sumSubarrayMins(array $arr): int {
        $n = count($arr);
        $left = array_fill(0, $n, 0);
        $right = array_fill(0, $n, 0);

        $stack = new \SplStack();

        for ($i = 0; $i < $n; $i++) {
            // Pop while stack is greater than or equal to target (because of possible duplicates)
            while (!$stack->isEmpty() && $arr[$stack->top()] >= $arr[$i]) $stack->pop();
            $top = $stack->isEmpty() ? 0 : $stack->top() + 1;
            $stack->push($i);
            $left[$i] = $top;
        }

        $stack = new \SplStack();

        for ($i = $n-1; $i >= 0; $i--) {
            // Pop while stack is greater than target
            while (!$stack->isEmpty() && $arr[$stack->top()] > $arr[$i]) $stack->pop();
            $top = $stack->isEmpty() ? $n-1 : $stack->top()-1;
            $stack->push($i);
            $right[$i] = $top;
        }

        $fn = static fn ($x) => ($x * ($x + 1)) / 2;
        $total = 0;
        for ($i = 0; $i < $n; $i++) {
            // The number of subarrays
            $count = $fn($right[$i] - $left[$i] + 1) - $fn($i-$left[$i]) - $fn($right[$i]-$i);
            // Add the total contribution of this element to total
            $total = ($total + ($count * $arr[$i])) % self::MOD;
        }

        return $total;
    }
}

As you can see, if we unreveal the non-trivial math tricks used here, the solution and concept behind this is very simple. I can imagine that well trained candidate will manage to do this in an interview, but for me it was definitely very hard to crack by myself (needed the hint for monotonic stack to be honest).

I hope you've liked this post and deepened your understanding of used concepts.